Két évvel ezelőtt készült már egy hasonló bejegyzés, amiért ismét megemlítem, annak az oka a következő: Rájöttem, hogy a mostani osztályomnál nem elég egy dolgot elmondani kétszer vagy háromszor, de még tízszer sem.
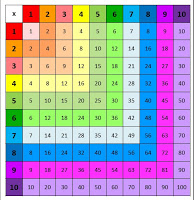
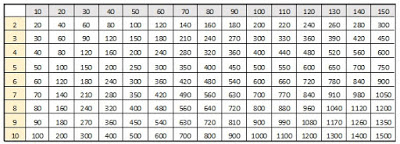
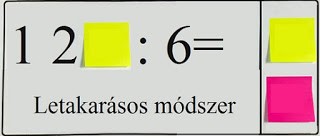
A szóbeli szorzás – osztás bevezető óráin mutattam a gyerekeknek, hogy bizonyos analógiát követve ugyanúgy osztjuk mondjuk a nyolcat kettővel, mint a nyolcvanat, vagy a nyolcszázat. Beszéltem nekik a „zéró-héró” módszerről, illetve a „letakarásos” módszerről. Úgy látszott, megértették.
Mondtam nekik, hogy minden osztásnál ezt kell figyelni, és a kettő közül valamelyiket alkalmazni. Mikor a héten jobban belemélyedtünk volna az osztásba, úgy néztek rám, mint az a bizonyos kisborjú az új kapura.
Vagy letakartak, vagy nem, vagy figyelembe vették, vagy nem. Szóval káoszháza. Sőt, most már olyan osztások is jöttek, ahol nem volt letakarható vagy áthúzható nulla.
A szorzásnál tanultak szerint akartak volna bontani, ami persze osztásnál nem működik. Ekkor eszembe jutott a szorzótáblánál használt számtábla.
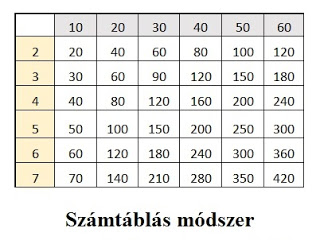
Ezt módosítottam egy kicsit, és most ez az úgynevezett „táblázatos módszer”.
Ha például a feladat: 92 : 4, akkor a számtáblán megkeressük a 4-es sort. A soron vezetve az ujjunkat keressük azt a számot, ami kerek tízes, és a 92 környékén van. Jelen esetben megtaláljuk a 80-at. Ha felvisszük az ujjunkat a 80-as oszlopon, a 20-hoz jutunk. Ez lesz a bontásunk alapja, illetve a részeredmény.
Ezután a 92-ből elvesszük a nyolcvanat, és a maradékot osztjuk el 4-gyel. A két részeredményt összeadva kapjuk a végeredményt.
Miután rájöttem a gyerekek korlátaira, azóta minden órán megbeszéljük, hogy az immár háromra emelkedett módszer közül melyik feladatnál melyiket kell majd használni. Készítettem kártyákat is, így remélhetőleg belevésődik a fejükbe a három módszer, és használni is tudják majd.
Ha a Ti tanítványaitoknak, gyermekeiteknek is problémája van az osztással, próbáljátok ki velük ezeket a „módszereket”, hátha náluk is beválik!
Jó tanulást!
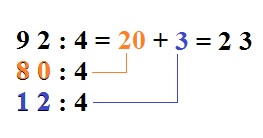

Nagyszeru ötletek! En Angliában tanitom a szorzotablat, sajnos sokan meg ötödik osztályban sincsenek vele tisztában. A letakarasos módszert mindenképp ki fogom próbálni! Köszönöm a megosztást.
Köszönöm szépen. Remélem hasznos lesz nektek is. :))